- 난이도 : 실버 1(solved.ac 기준)
- 언어 : java

문제 요약
N = 1일 때 배열을 Z 모양 순으로 탐색하고 N > 1일 경우
배열을 4등분한 후 재귀적으로 순서대로 방문하고 (r,c)을 몇 번째로 방문하는지 구하여라.유의 사항
재귀함수를 쓰는 만큼 기저 조건을 잘 써주자.
그리고 (r,c)는 (x,y)가 아닌 (y,x)이다. 따라서 (c,r)로 생각하여 풀자.
(단, 0 <= r,c < 2N)문제 풀이
이 문제는 재귀함수를 사용하여 분할정복하여야 한다.
N>1 일 때 2x2 배열이 될 때 문제의 그림처럼 계속하여 분할해주어야하기 때문이다.
예시) 8x8 -> 4x4(4개) -> 2x2(16개)
재귀함수를 실행하면서 2x2인지 확인을 하고 아닐 경우 2x2이 될 때까지 재귀함수를 실행한다.
그리고 2x2 배열을 Z 모양으로 탐색하여 (r,c)을 찾을 때까지 카운팅 해준다.
나는 여기서 4등분한 배열의 각 끝점이 r이나 c보다 작을 경우 더 분할하지 않고 바로 전체를 카운팅해주었다.
왜 그런지는 그림으로 설명해주겠다.

N=3, r=6, c=2일 경우 배열 a는 23 = 8인 a[8][8]의 배열을 가지게 된다.
그리고 찾아야할 좌표는 (c, r)인 (2,6)이다.
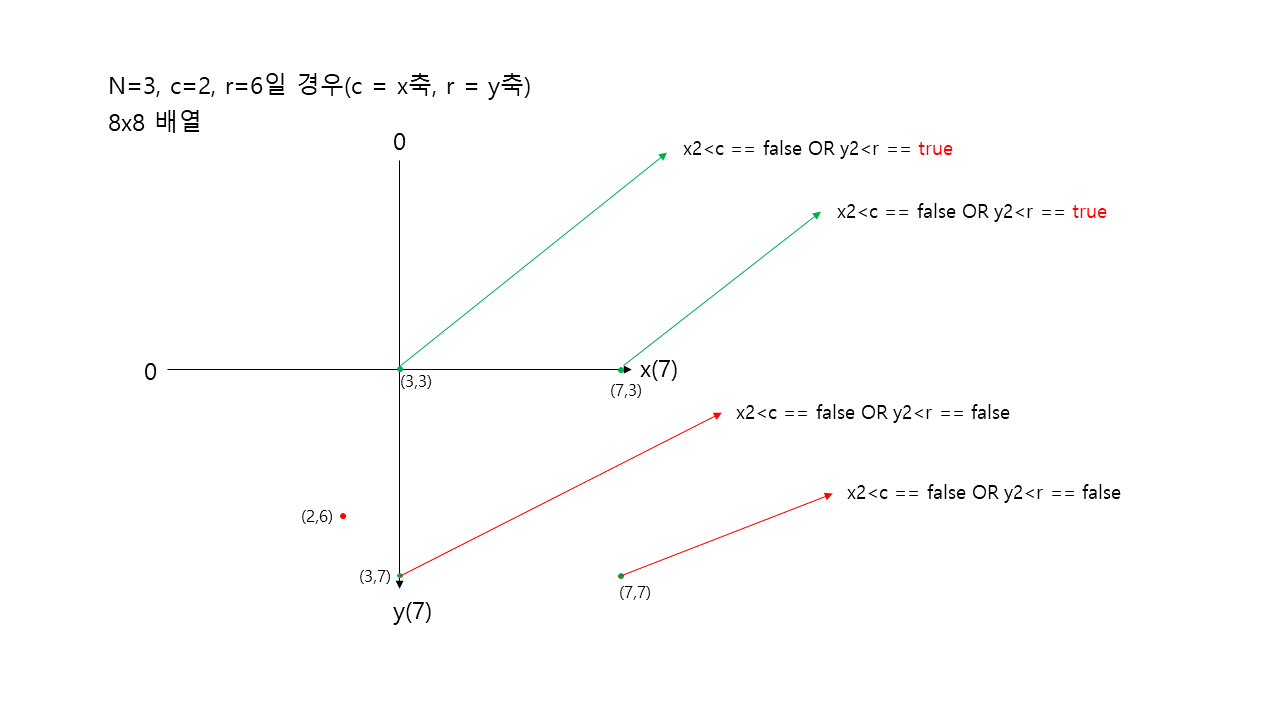
N>1이기 때문에 배열을 4등분하여 각 끝점이 r이나 c보다 작을 경우를 살펴본다.
찾는 좌표 위치가 3사분면이기 때문에 1,2사분면은 3사분면보다 y값이 작을 수 밖에 없다.
(단, 그래프상 y는 아래로 갈수록 커짐)

따라서 1,2사분면은 더이상 분할하여 재귀함수를 실행할 필요도 없이 모두 탐색했다고 가정하여 카운팅해준다.

현재 8x8배열이라서 2개의 4x4배열이 만들어지고 하나의 4x4의 배열은 4개의 2x2배열이 만들어진다.
2x2배열의 원소 수는 총 4개이기에 한사분면의 원소 수는 4*4 = 16개가 된다.

1,2사분면의 원소 수의 합을 더하면 16*2 = 32가 카운팅 된다.
이제는 3사분면을 탐색해야한다.

3사분면은 4x4배열이기 때문에 또다시 분할시켜준다.
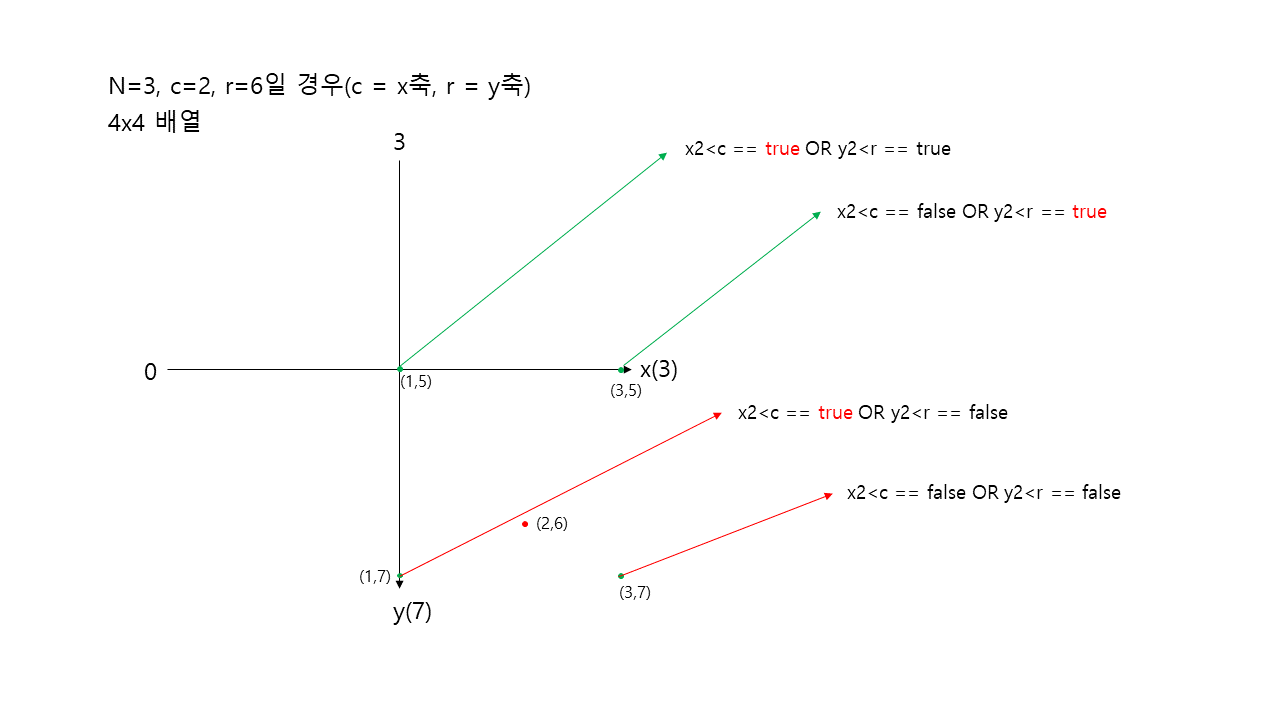
분할 결과 찾는 좌표가 4사분면에 있기에 1,2사분면의 경우 y값이 작고 3사분면의 경우 x값이 작다.
(4사분면 대비)

따라서 1,2,3사분면은 더이상 분할하여 재귀함수를 실행할 필요도 없이 모두 탐색했다고 가정하여 카운팅해준다.

이제는 4x4배열이라서 총 3개의 2x2배열이 만들어진다.

2x2배열의 원소 수는 총 4개이다. 따라서 총 원소 수는 4*3 = 12개가 된다.
이전에 카운트한 32에서 12를 더하여 총 44번의 탐색을 한 셈 치는 것이다.

이제 남은 4사분면을 탐색해주어야하지만 2x2배열은 Z방향으로 탐색해준다.
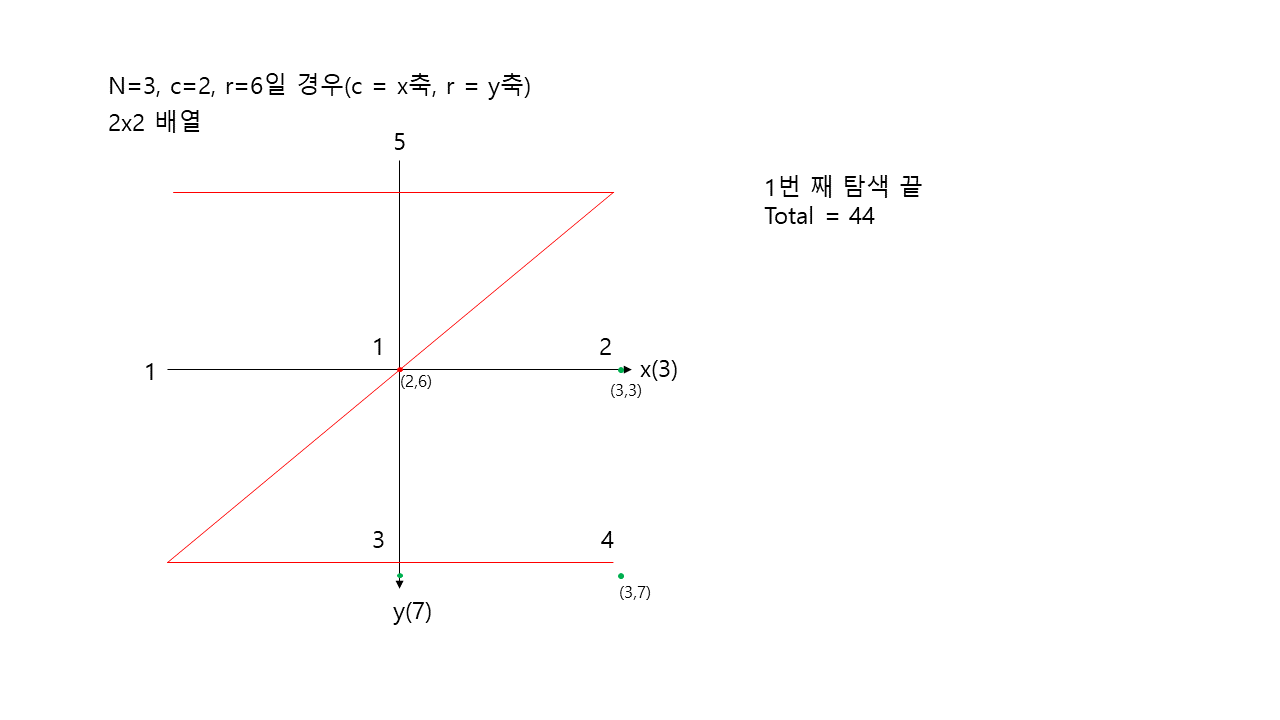
처음에 바로 원하는 좌표가 탐색이 되었기 때문에 카운팅하지 않고 탐색을 끝낸다.
- 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61import java.io.*;
import java.util.*;
public class Main {
static int N, r, c, cnt = 0;
static boolean isFind = false;
private static void find(int startX, int startY, int endX, int endY) {
if ((endY - startY + 1) / 2 >= 2) {
int x1, x2, y1, y2;
for (int i = 0; i < 4; i++) {
if (i % 2 == 1) {
x1 = (endX + startX) / 2 + 1;
x2 = endX;
} else {
x1 = startX;
x2 = (endX + startX) / 2;
}
if (i > 1) {
y1 = (endY + startY) / 2 + 1;
y2 = endY;
} else {
y1 = startY;
y2 = (endY + startY) / 2;
}
if (y2 < r || x2 < c) {
cnt += (x2 - x1 + 1) * (y2 - y1 + 1);
} else
find(x1, y1, x2, y2);
if (isFind)
return;
}
} else {
for (int i = startY; i < endY + 1; i++) {
for (int j = startX; j < endX + 1; j++) {
if (i == r && j == c) {
isFind = true;
return;
} else
cnt++;
}
}
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
r = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
int maxSize = (int) Math.pow(2, N) - 1;
find(0, 0, maxSize, maxSize);
bw.write(cnt + "\n");
bw.flush();
bw.close();
br.close();
}
} - 후기
분할을 어떻게 해야할 것인가부터 재귀를 어떻게 정상적으로 실행할 것인가까지 고민할 수 있게 만들어 준 문제
기존에는 처음부터 좌표를 찾을 때까지 분할하여 탐색하는 방식으로 풀었지만 생각보다 시간이 오래 걸려서 추가로 위의 조건을 추가하여 주었다.

